Перестановки, сочетания и размещения без повторений. Комбинаторика - основные понятия и формулы

Рассмотрим множество А = {а1, а2,..., аn}, содержащее n различных элементов, которое будем называть n-множеством
или генеральной совокупностью объема n. Из n-множества можно образовать его части (подмножества).
Определение. Подмножество, состоящее из m элементов n-множества, называют m-подмножеством n-множества или со-
единением из n элементов по m, или выборкой объема m из генеральной совокупности объема n.
Возможны два способа выбора:

1. Выбор без возвращения, при котором однажды выбранный элемент удаляется из генеральной совокупности. Выборка
(соединение) в этом случае не содержит повторяющихся элементов.

2. Выбор с возвращением, при котором выбор производится каждый раз из всей генеральной совокупности, то есть перед
следующим выбором предыдущий выбранный элемент возвращается в генеральную совокупность. В выборке (соединении) в
этом случае встречаются повторения.

Какие выборки одного и того же объема считать различными и какие одинаковыми, зависит от правил выбора соедине-
ния (подмножества, выборки).
Два соединения могут отличаться либо 1) составом, если они содержат хотя бы по одному различному элементу, либо
2) порядком входящих элементов.
В зависимости от правил выбора соединения делят на три типа: размещения, перестановки, сочетания. В зависимости от
способа выбора (без возвращения или с возвращением) каждый тип соединения может быть без повторений или с повторениями.

2. Размещения без и с повторениями.

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно
выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой
можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов,
среди которых есть одинаковые?

Определение. Размещениями из n элементов по m называются соединения из n элементов по m, которые отличаются
друг от друга либо своими элементами (составом), либо порядком их расположения.

На языке теории множеств это звучит следующим образом: размещения из n элементов по m – это упорядоченное
m-подмножество n-множества (упорядоченная m-выборка из генеральной совокупности объема n). Термин «упорядоченная»
означает, что порядок следования элементов в выборке существенен: выборки с одними и теми же элементами, но с разным
порядком их следования различны.

Задача . Пусть имеется множество, содержащее 4 буквы:
{А, B, C, D}. Записать все возможные размещения из 4 указанных букв по две:

а) без повторений;

б) с повторениями.

Решение.

а) Таких размещений 12: (АВ), (AC), (АD), (ВС),(ВD), (BA), (CA), (CB), (СD), (DА), (DВ), (DС). Заметим, что
размещения отличаются порядком входящих в них элементов и их составом. Размещения АВ и ВА содержат одинаковые буквы,
но порядок их расположения различен.
б) Таких размещений 16. К приведенным для случая (а)
размещениям добавляются размещения из одинаковых элементов (АА), (BB), (CC), (DD).

Задача . Пусть имеется множество, содержащее 2 буквы:{A, B}. Записать все возможные размещения с повторениями из
4-х букв.
Решение. Таких размещений 16: (AAAA), (BBBB), (AAAB),(AABA), (ABAA), (BAAA), (AABB), (ABAB), (BABA), (BBAA), (ABBA),
(BAAB), (BBBA), (BBAB), (BABB), (ABBB).

Теорема 3. 3.1 Число различных размещений без повторений из n элементов по m равно

для выборки без возвращения.

3.2 Число размещений с повторениями из n элементов по m равноm (2) для выборки с возвращением.

Доказательство. Для доказательства воспользуемся пра- вилом умножения.

Рассмотрим выборки без возвращения. Для выбора первого элемента имеется n возможностей, второго – (n – 1)

(перед вторым выбором в генеральной совокупности ос- талось (n –1) элементов),..., при m-ом выборе (n – m + 1) воз- можностей.

Таким образом, по правилу умножения

Запишем выражение в более удобном виде, умножив и разделив его на (m – n)!

Считается, что 0! = 1, что позволяет использовать эту формулу для случая m = n.

Рассмотрим выборки с возвращением . Для выбора первого элемента имеется n возможностей, второго – тоже n (перед выбо-
ром очередного элемента предыдущий выбранный элемент зафиксирован и возвращен в генеральную совокупность), при m-м вы-
боре тоже n возможностей. Таким образом .

Задача . В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии.

Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение . В данной задаче генеральной совокупностью являются 12 страниц газеты, и выборкой без возвращения 4 выбранные из них страницы для фотографий. В данной задаче важно не только то, какие выбраны страницы, но и в каком порядке (для расположения фотографий). Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Задача . У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих
штампов нанести на все книги пятизначные номера – составить каталог. Сколько различных пятизначных номеров может со-
ставить мальчик?
Решение. Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр {1, 3, 7}. Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

3. Перестановки без повторений
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно
выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Определение. Размещения, в которых участвуют все n элементов генеральной совокупности, называются перестанов-
ками без повторений из n элементов. Перестановки состоят из одних и тех же элементов, но отличаются между собой порядком.

Задача . Пусть имеется множество букв {A, B, C}. Записать все возможные перестановки.
Решение. Этому множеству букв соответствует 6 перестановок: (АВС), (ACB), (BAC), (BCA), (CBA), (CAB).

Теорема . Число перестановок n различных элементов равно n!, т. е. Рn = n!

Доказательство. Так как перестановки являются частным случаем размещений, то при n = m получаем

Замечание. При больших n для подсчета факториала исполь- зуют таблицу логарифмов факториалов либо приближенную формулу Стирлинга

Задача . Сколько можно составить четырехбуквенных «слов» из букв слова «брак»?

Решение . Генеральной совокупностью являются 4 буквы слова «брак» {б, р, а, к}.

Число «слов» определяется перестановками этих 4 букв, т. е. Р4 = 4! = 1 x 2 x 3 x 4 = 24.

Задача . Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение . В исходной генеральной совокупности – 9 разных книг.

Тогда для остальных 6 книг существует Р6 = 6! = 720 перестановок.

Однако четыре определенные книги можно переставить между собой Р4 = 4! = 24 способами.

По правилу умножения имеем Р6 x Р4 = 720 x 24 = 17280.

4. Перестановки с повторениями
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на
n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Определение. Перестановками с повторениями называются соединения из генеральной совокупности, каждое из которых содержит n элементов, среди которых элемент

а1 повторяется n1 раз,
а2 повторяется n2 раз,
. . . . . . . . . . . . . . . . . . .
аn повторяется nk раз
n1 + n2 + ... + nk = n
и которые отличаются друг от друга только порядком расположения различных элементов.

Теорема. Число перестановок с повторениями

Доказательство. Доказательство очевидно, так как перестановки одинаковых элементов в перестановке с повторениями не дают новой перестановки.

Задача .

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение. Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв.

Следовательно, число перестановок с повторениями равно

5. Сочетания без повторений
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из п различных предметов?
Определение. Сочетаниями из n различных элементов по m называются соединения из n элементов по m (m <=n), которые
отличаются друг от друга только составом элементов.

Задача. Пусть имеется множество, содержащее 4 буквы {A, B, C, D}. Запишем все возможные сочетания из указанных
букв по 3.
Решение. Таких сочетаний 4: ABC, ACD, ABD, BCD.
Здесь в число сочетаний не включены, например, АСВ,ВСА, так как они не отличаются по составу от последовательно-
сти букв АВС, потому что перестановка элементов нового сочетания не дает.

Теорема. Число сочетаний из n элементов по m равно

Доказательство.

Вспомним, что и сочетания, и размещения из n элементов по m – это выборки объема m из генеральной совокупности объема n и разница между ними в том, что в случае размещений важен и состав, и порядок элементов, тогда как в случае сочетаний важен только состав элементов. Пусть имеется какое-то одно сочетание. Для того, чтобы образовать все размещения с такими же элементами, нужно осуществить всевозможные перестановки элементов этого сочетания. Поскольку в сочетании m элементов, то существует m! перестановок. Следовательно, одному сочетанию, состоящему из m элементов, соответствует m! размещений с этими элементами. Поэтому

Числа называются биномиальными коэффициентами: они являются коэффициентами в разложении бинома Ньютона

Задача . Необходимо выбрать в подарок 4 из 10 имеющих- ся различных книг. Сколькими способами можно это сделать?

Решение . Генеральной совокупностью является 10 раз- личных книг. Из них нужно выбрать 4, причем порядок выбора книг не играет роли. Нужно найти число сочетаний из 10 элементов по

Задача . Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?

Решение . Имеем 15 шаров: 10 белых и 5 черных. Нужно выбрать 7 шаров: 4 белых и 3 черных.

Разобьем 15 шаров на 2 генеральные совокупности:

1) 10 белых шаров;

2) 5 черных шаров.

4 белых шара будем выбирать из I генеральной совокупности, порядок выбора безразличен, их можно выбрать

Способами. 3 черных шара будем выбирать из II генеральной совокупности, их можно выбрать

Способами.

Тогда по правилу умножения искомое число способов равно .

Решение этой задачи можно схематически представить следующим образом

Задача . Десять команд участвуют в розыгрыше первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е место.

Две команды, занявшие последние места, не будут участвовать в следующем таком же первенстве.

Сколько разных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд.

Решение . Имеется генеральная совокупность объема 10 команд. Из нее будем выбирать 5 команд в 2 этапа:

1) сначала на первые 3 места из 10 с учетом состава и порядка команд;

2) затем на последние 2 места из оставшихся 7 с учетом только состава (порядок выбывших команд не важен).

Первые 3 места могут быть распределены способами.

Число способов исключить 2 команды из оставшихся 7 равно .

Согласно правилу умножения получаем, что число разных результатов неравенства равно 0.

Задача .

Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни одни из них не будет подверг нут опросу дважды и на занятии может быть опрошено любое количество учащихся, причем порядок, в котором опрашивают- ся учащиеся, безразличен?

Решение .

I способ. Имеется генеральная совокупность объема 11 учащихся. Преподаватель может не опросить ни одного из 11 учащихся, что является одним из вариантов. Этому случаю соответствует . Преподаватель может опросить только одного из учащихся, таких вариантов .

Если преподаватель опросит двух учащихся, то число вариантов опроса . Для опроса трех учащихся существует вариантов и т. д.

Наконец, могут быть опрошены все учащиеся. Число вариантов в этом случае .

Число всех возможных вариантов опроса можно найти по пра- вилу сложения

Решение этой задачи можно схематически представить следующим образом:

II способ. Имеется генеральная совокупность, состоящая из 2 элементов:

{а, в}, где а – ученик опрошен, в – ученик не опрошен на данном занятии.

Опыт состоит в 11-кратном выборе с возвращением одного из элементов этого множества – каждый из 11 учеников либо опрошен, либо не опрошен.

В данной задаче важно не только то, какие выбраны элементы множества (сколько учеников опрошено и сколько нет),

но и в каком порядке (т. е. какой именно ученик опрошен или нет).

Число способов такого выбора определяется числом размещений с повторениями из 2 элементов по 11; .

6. Сочетания с повторениями
Рассмотрим задачу о числе сочетаний с повторениями:
имеется по r одинаковых предметов каждого из n различных типов;

сколькими способами можно выбрать m (m <= r) из этих (n x r) предметов?

Определение . Сочетаниями с повторениями называются соединения из n элементов по m (выбор с возвращением m элементов), которые отличаются только составом и при этом отдельные соединения могут содержать повторяющиеся элементы.

Задача . Имеются 2 буквы А, 2 буквы В, 2 буквы С. Сколькими способами можно выбрать две из этих шести букв?
Решение. Существует 6 способов выбора 2 букв из 6 с повторениями: (АА), (AB), (AC), (BC), (BB), (CC). Порядок следо-
вания букв не учитывается.

Теорема . Число сочетаний с повторениями равно

Доказательство. Пусть имеются предметы n различных типов. Сколько соединений по m элементов можно из них сделать, если не принимать во внимание порядок элементов. Расположим в каждом сочетании элементы по типам (сначала все элементы 1-го типа, потом 2-го и т. д.). После этого перенумеруем все элементы в сочетании, но к номерам элементов второ- го типа прибавим 1, третьего типа – 2 и т. д. Тогда из каждого сочетания с повторениями получится сочетание без повторений, состоящее из чисел 1, 2,..., n + m – 1, причем в каждое сочетание входит m элементов.

Отсюда следует, что

Задача . В технической библиотеке имеются книги по ма- тематике, физике, химии и т. д., всего по 16 разделам науки.

Поступили очередные 4 заказа на литературу. Сколько сущест- вует вариантов такого заказа?

Решение. Так как 4 заказанные книги могут быть и из одно- го раздела науки, и из разных разделов, при этом порядок выбора разделов не важен, то число вариантов заказа определяется чис- лом сочетаний с повторениями из 16 элементов по 4, т. е.

Задача . В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение . Очевидно, что порядок, в котором выбираются пирожные, не существен, причем в комбинации могут входить повторяющиеся элементы (например, можно купить 7 эклеров). Следовательно, число способов покупки 7 пирожных определяется числом сочетаний с повторениями из 4 элементов по 7, т. е

7. Комбинаторика разбиений

Рассмотрим в этом классе задач две следующие задачи:

1. Даны n различных предметов и k различных групп. Сколькими способами можно распределить n различных предметов по k различным группам, если допускаются пустые группы. Ниже покажем, что число способов равно k^n .

2. Даны n различных предметов и k различных групп. Сколькими способами можно распределить n различных пред- метов по k группам, если в первой группе n1 предметов, во второй – n2 , в k-й – nk , где n1 + n2 +... + nk = n . Ниже покажем, что число способов равно

Рассмотрим решение первой задачи. Пусть генеральной совокупностью будет k различных групп {1, 2,..., k}. Можно считать, что опыт состоит в n-кратном выборе с возвращением номера группы для каждого предмета. Заметим, что поскольку предметы разные, то важно не только, какие группы выбираются для предметов, но и в каком порядке выбираются эти группы. Таким образом, число способов раз- бить n различных предметов на k групп определяется числом размещений с повторениями и k элементов по n:

Рассмотрим решение второй задачи.

Разбиение n предметов по k группам можно выполнить следующим образом. Сначала положим все n предметов в ряд. После этого возьмем первые n1 предметов и поместим их в первую группу, вторые n2 предмета – во вторую группу, ..., последние nk предметов в k-ю группу. Ясно, что меняя положение предметов в ряду, можно получить всевозможные разбиения предметов. Так как число перестановок из n элементов равно n!, то число расположения предметов в ряд равно n! При этом заметим, что любая перестановка первых n1 предметов ничего не меняет, так же как и вторых n2, ..., и последних nk. В силу правила произведения получим n1!n2!...nk! перестановок предметов, не меняющих результата раздела. Таким образом, число способов разбиения на группы равно

Формула совпадает с формулой для числа перестановок с повторениями. К этому же результату можно прийти иначе. Первые n1 предметов выбираем из n предметов. Так как порядок выбранных предметов безразличен, то имеет выборов. После этого следующие n2 предмета выбираем из оставшихся n – n1. Это можно сделать способами, и т. д.

Наконец, последние nk предметов выбираем из оставшихся nk. Это можно сделать , т. е. единственным способом. По правилу произведения получаем, что число способов разбиения на группы равно

Как видим, задачи о разбиениях привели к уже известным формулам комбинаторики.

Задача. 7 одинаковых шариков случайным образом рас- сыпаются по 4 лункам (в одну лунку может поместиться любое число шаров). Сколько существует различных способов распре- деления 7 шариков по 4 лункам?

Решение. Мы имеем 7 шариков, которые распределяем по 4 лункам (лунки могут быть пустые), т. е. это соответствует первой задаче о разбиениях, число способов равно 4^7 = 16348

Задача. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Решение. Это задача о разделе 28 костей между 4 игрока- ми по 7 костей. Используя полученную выше формулу для числа способов такого раздела (задача 2), имеем

8. Рекомендации по решению задач
Решение комбинаторных задач представляет известную трудность для начинающих. Причин много, но одна из них очевидна – при изложении комбинаторики используется своя специфическая терминология (генеральная совокупность, выборка, правила выбора). В задаче же этих терминов, как правило, нет –сформулирована она на обычном литературном языке и комби-

наторные понятия присутствуют в ней в неявной форме. Поэтому после усвоения содержания задачи нужно ее «перевести»
на математический язык.
Для этого необходимо выяснить,
1) что является генеральной совокупностью - она всегда будет присутствовать в задаче, т. е. комбинаторные задачи свя-
заны с выбором объектов, а этот выбор из чего-то (генеральной совокупности) производится; каков объем генеральной сово-
купности;
2) одна или несколько генеральных совокупностей;
3) что является выборкой и каков объем выборки;
4) правила выбора: допустимы или нет повторы, важен ли порядок выбираемых элементов, возможно ли изменение состава.
После этого полезно для себя переформулировать задачу на языке генеральных совокупностей и выборок. В зависимости
от ситуации выбрать нужную формулу (см. таблицу). Иногда в более сложных задачах приходится использовать совместно не-
сколько формул.

В заключение приведем основные свойства чисел .

Прежде всего, построим таблицу таких чисел, используя формулу (3.11).

Таблица чисел имеет треугольную форму и называется треугольником Паскаля по имени математика Блеза Паскаля (1623-1662). Анализируя треугольник Паскаля, легко видеть основные свойства чисел .

Свойства 1 – 2 вытекают из определения сочетания как подмножества, содержащего m элементов множества, имеющего n элементов.

Свойства 3 – 5 доказываются методом математической индукции.

В силу свойства 4 треугольник Паскаля легко продолжить вниз на любое число шагов.

рис 3.2 схема определения вида расстановок и выбора формул

Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики : сочетания, размещения, перестановки (смотрите ) и научиться их применять для решения задач.

Как выбрать формулу комбинаторики?

Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:

• алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
• рекомендации по изучению комбинаторики,
• 6 задач с решениями и комментариями на каждую формулу.

Перестановки

Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками , а их число равно

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Пример всех перестановок из $n=3$ объектов (различных фигур) - на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).

Размещения

Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями

$$A_n^m=\frac{n!}{(n-m)!}=n\cdot (n-1)\cdot ... \cdot (n-m+1) $$

Пример всех размещений из $n=3$ объектов (различных фигур) по $m=2$ - на картинке справа. Согласно формуле, их должно быть ровно $A_3^2=3\cdot (3-2+1)=3\cdot 2 =6$.

Сочетания

Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $m$, а их число равно

$$C_n^m=\frac{n!}{(n-m)!\cdot m!} $$

Пример всех сочетаний из $n=3$ объектов (различных фигур) по $m=2$ - на картинке справа. Согласно формуле, их должно быть ровно $C_3^2=\frac{3!}{(3-2)!\cdot 2!} =3$. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем именно в $m!$ раз, то есть верна формула связи:

$$ A_n^m = C_n^m \cdot P_m.$$

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Рождение комбинаторики как раздела связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.

Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.

Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.

Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.

В дальнейшем важную роль будет играть следующая

Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .

Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.

Размещения, перестановки, сочетания

Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .

Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .

Теорема. Число размещений множества из элементов по элементов равно

Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов — это

Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки ладей

По определению!

Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа

Все сочетания из множества по два — .

Свойства чисел {\sf C}_n^k

Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.

Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .

Треугольник Паскаля

В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

Теорема.

Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?

1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член

2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке

Домножим числитель и знаменатель этой дроби на :

Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?

Искомое число способов

Задачи.

1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :

Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.

Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?

Перестановка – это комбинация элементов из N разных элементов взятых в определенном порядке. В перестановке важен порядок следования элементов, и в перестановке должны быть задействованы все N элементов.

Задача : Найти все возможные перестановки для последовательности чисел 1, 2, 3.
Существуют следующие перестановки:

1: 1 2 3
2: 1 3 2
3: 2 1 3
4: 2 3 1
5: 3 1 2
6: 3 2 1

Перестановки без повторений

Количество перестановок для N различных элементов составляет N! . Действительно:

• на первое место может быть помещен любой из N элементов (всего вариантов N ),
• на вторую позицию может быть помещен любой из оставшихся (N-1) элементов (итого вариантов N·(N-1) ),
• если продолжить данную последовательность для всех N мест, то получим: N·(N-1)·(N-2)· … ·1 , то есть всего N! перестановок.

Рассмотрим задачу получения всех перестановок чисел 1…N (то есть последовательности длины N ), где каждое из чисел входит ровно по 1 разу. Существует множество вариантов порядка получения перестановок. Однако наиболее часто решается задача генерации перестановок в лексикографическом порядке (см. пример выше). При этом все перестановки сортируются сначала по первому числу, затем по второму и т.д. в порядке возрастания. Таким образом, первой будет перестановка 1 2 … N , а последней — N N-1 … 1 .

Рассмотрим алгоритм решения задачи. Дана исходная последовательность чисел. Для получения каждой следующей перестановки необходимо выполнить следующие шаги:

• Необходимо просмотреть текущую перестановку справа налево и при этом следить за тем, чтобы каждый следующий элемент перестановки (элемент с большим номером) был не более чем предыдущий (элемент с меньшим номером). Как только данное соотношение будет нарушено необходимо остановиться и отметить текущее число (позиция 1).
• Снова просмотреть пройденный путь справа налево пока не дойдем до первого числа, которое больше чем отмеченное на предыдущем шаге.
• Поменять местами два полученных элемента.
• Теперь в части массива, которая размещена справа от позиции 1 надо отсортировать все числа в порядке возрастания. Поскольку до этого они все были уже записаны в порядке убывания необходимо эту часть подпоследовательность просто перевернуть.

Таким образом мы получим новую последовательность, которая будет рассматриваться в качестве исходной на следующем шаге.

Реализация на С++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include
using namespace std;

{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n - 2;
while (j != -1 && a[j] >= a) j--;
if (j == -1)
return false; // больше перестановок нет
int k = n - 1;
while (a[j] >= a[k]) k--;
swap(a, j, k);
int l = j + 1, r = n - 1;
while (l swap(a, l++, r--);
return true;
}
void Print(int *a, int n) // вывод перестановки
{
static int num = 1; // номер перестановки
cout.width(3);
cout << num++ << ": " ;
for (int i = 0; i < n; i++)
cout << a[i] << " " ;
cout << endl;
}
int main()
{
int n, *a;
cout << "N = " ;
cin >> n;
a = new int [n];
for (int i = 0; i < n; i++)
a[i] = i + 1;
Print(a, n);
while (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
return 0;
}

Результат выполнения

Перестановки с повторениями

Особого внимания заслуживает задача генерации перестановок N элементов в случае если элементы последовательности могут повторяться. Допустим, исходная последовательность состоит из элементов n 1 , n 2 ... n k , где элемент n 1 повторяется r 1 раз, n 2 повторяется r 2 раз и т.д. При этом n 1 +n 2 +...+n k =N . Если мы будем считать все n 1 +n 2 +...+n k элементов перестановки с повторениями различными, то всего различных вариантов перестановок (n 1 +n 2 +...+n k)! . Однако среди этих перестановок не все различны. В самом деле, все r 1 элементов n 1 мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы n 2 , n 3 и т. д. В итоге имеем r 1 ! вариантов записи одной и той же перестановки с различным расположением повторяющихся элементов n 1 . Таким образом, всякая перестановка может быть записана r 1 !·r 2 !·...·r k ! способами. Следовательно, число различных перестановок с повторениями равно

Для генерации перестановок с повторениями можно использовать алгоритм генерации перестановок без повторений, приведенный выше. Введем повторяющийся элемент в массив a. Ниже приведен код программы для генерации перестановок с повторениями (изменен только код функции main() ).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#include
using namespace std;
void swap(int *a, int i, int j)
{
int s = a[i];
a[i] = a[j];
a[j] = s;
}
bool NextSet(int *a, int n)
{
int j = n - 2;
while (j != -1 && a[j] >= a) j--;
if (j == -1)
return false; // больше перестановок нет
int k = n - 1;
while (a[j] >= a[k]) k--;
swap(a, j, k);
int l = j + 1, r = n - 1; // сортируем оставшуюся часть последовательности
while (l swap(a, l++, r--);
return true;
}
void Print(int *a, int n) // вывод перестановки
{
static int num = 1; // номер перестановки
cout.width(3); // ширина поля вывода номера перестановки
cout << num++ << ": " ;
for (int i = 0; i < n; i++)
cout << a[i] << " " ;
cout << endl;
}
int main()
{
int n, *a;
cout << "N = " ;
cin >> n;
a = new int [n];
for (int i = 0; i < n; i++)
a[i] = i + 1;
a = 1; // повторяющийся элемент
Print(a, n);
while (NextSet(a, n))
Print(a, n);
cin.get(); cin.get();
return 0;
}

Результат работы приведенного выше алгоритма:

Задача . Определить количество всех упорядоченных наборов длиныr , которые можно составить из элементов множестваX (
), если выбор каждого элемента
, производится из всего множестваX .

Упорядоченный набор
– это элемент декартова произведения
, состоящего изr одинаковых множителейX . По правилу произведения количество элементов множества
равно
. Мы вывели формулу
.

Пример . Сколько четырехзначных телефонных номеров можно составить, если использовать все десять цифр?

Здесь
, и количество телефонных номеров равно

2.1.5. Размещения без повторений

Задача . Сколько упорядоченных наборов
можно составить изn элементов множестваX , если все элементы набора различны?

Первый элемент можно выбратьn способами. Если первый элемент уже выбран, то второй элементможно выбрать лишь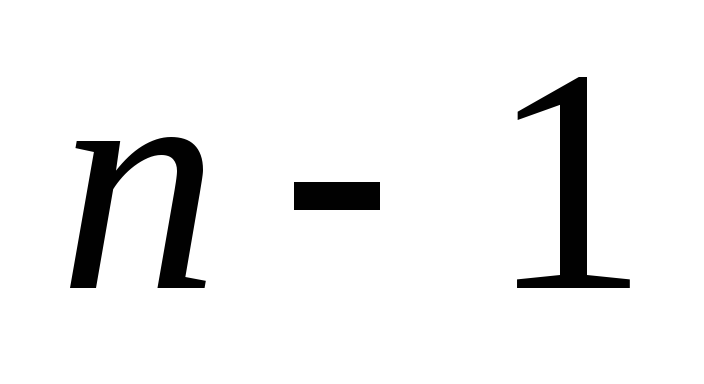
способами, а если уже выбран
элемент
, то элементможно выбрать
способами (повторение уже выбранного элемента не допускается). По правилу произведения получаем

Эта формула записывается иначе с использованием обозначения
. Так как

.

Пример . Сколько может быть различных списков победителей олимпиады (первое, второе, третье место), если участвовало 20 человек?

Здесь
, искомым является число

2.1.6. Перестановки без повторений

Рассмотрим частный случай размещения без повторений: если
, то в размещении участвуют все элементы множестваX , т.е. выборки имеют одинаковый состав и отличаются друг от друга только порядком элементов. Такие выборки называютсяперестановками . Количество перестановок изn элементов обозначают:

Пример. Сколькими способами можно выстроить очередь в кассу, если хотят получить зарплату шесть человек?

2.1.7. Перестановки с повторениями

Пусть множество X состоит изk различных элементов:
.Перестановкой с повторениями состава
будем называть упорядоченный набор длины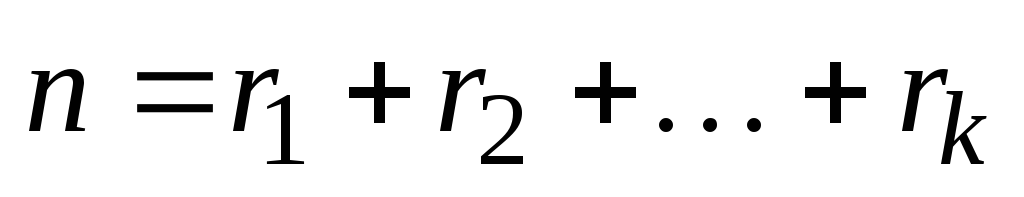
, в котором элементвстречается раз
. Количество таких перестановок обозначается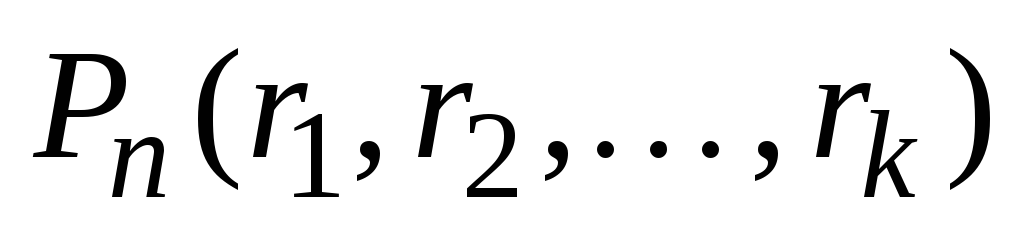
.

Пример . Из букв
запишем перестановку с повторением состава
. Ее длина
, причем букваa входит 2 раза,b – 2 раза,c – один раз. Такой перестановкой будет, например,
или
.

Выведем формулу количества перестановок с повторениями. Занумеруем все одинаковые элементы, входящие в перестановку, различными индексами, т.е. вместо перестановки
получим
. Теперь все элементы перестановки различны, а количество таких перестановок равно
. Первый элемент встречается в выборкераз. Уберем индексы у первого элемента (в нашем примере получим перестановку
), при этом число различных перестановок уменьшится в раз, т.к. при изменении порядка одинаковых элементов наша выборка не изменится. Уберем индексы у второго элемента – число перестановок уменьшится в раз. И так далее, до элемента с номеромk – число перестановок уменьшится в раз. Получим формулу

Пример . Сколько различных “слов” можно получить, переставляя буквы слова “передача” ?

В этом слове буквы “е” и “а” встречаются два раза, остальные по одному разу. Речь идет о перестановке с повторением состава
длины. Количество таких перестановок равно

2.1.8. Сочетания

Задача . Сколько различных множеств изr элементов можно составить из множества, содержащегоn элементов?

Будем составлять вначале упорядоченные наборы по r элементов в каждом. Количество таких наборов (это размещения изn элементов поr ) равно
. Теперь учитываем, что порядок записи элементов нам безразличен. При этом изразличных размещений, отличающихся только порядком элементов, получим одно сочетание. Например, два различных размещения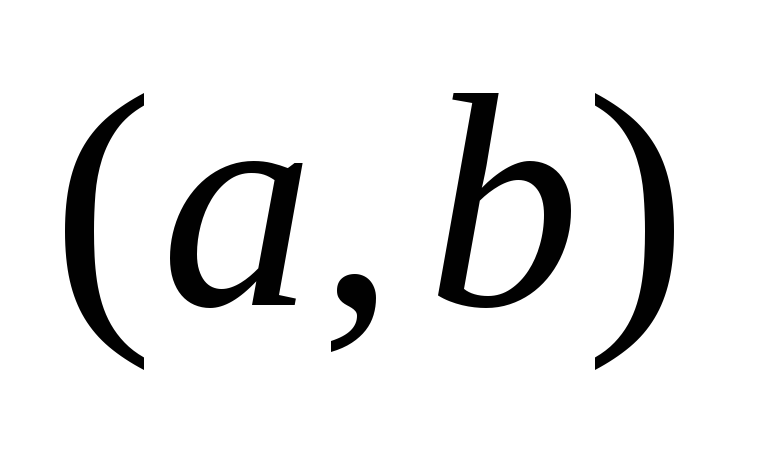
и
из двух элементов соответствуют одному сочетанию
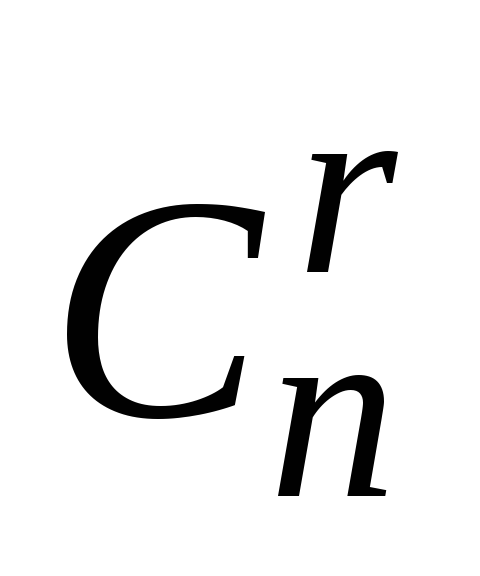. Таким образом, число сочетанийв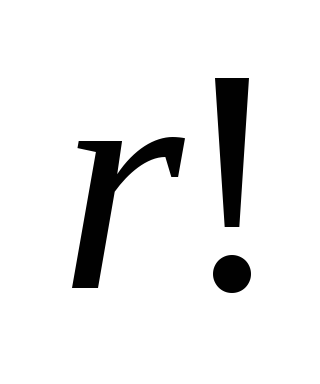раз меньше числа размещений:

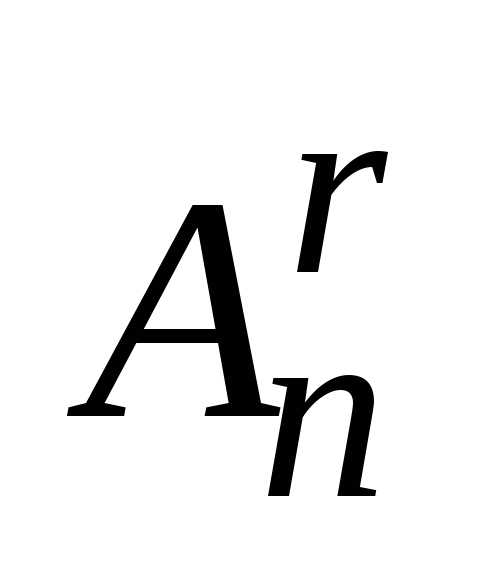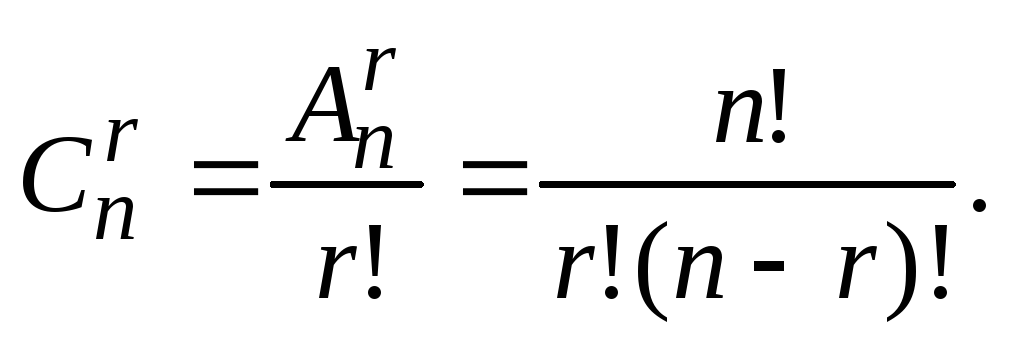
Пример . Количество способов, которыми мы можем выбрать из восьми дворников троих равно