Действия с десятичными дробями. Как решать десятичные дроби

В данной статье мы с Вами разберемся, что такое десятичная дробь, какие у нее есть особенности и свойства. Поехали! 🙂

Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).

Определение

Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.

Примеры дробей:

, ,

Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.

Представление дроби в десятичной записи

В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:

где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.

Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).

Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.

Пример:

Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.

В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.

Прочтение десятичных дробей

Часть Х читается в общем случае так: «Х целых».

Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉

Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.

Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.

3,5 читается как «три целых пять десятых»
0,016 читается как «ноль целых шестнадцать тысячных»

Перевод произвольной обыкновенной дроби в десятичную

Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.

Существует 2 способа перевода.

Первый способ перевода

Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.

Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.

Второй способ перевода

2-й способ заключается в делении числителя на знаменатель в столбик или на калькуляторе. Целая часть, если таковая имеется, в преобразовании не участвует.

Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).

Перевод десятичной дроби в обыкновенную

Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.

Конечная и бесконечная десятичная дробь

Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.

Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.

В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:

как результат сокращения до желательного количества разрядов после запятой;
в виде периодической дроби.

Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.

Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).

Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби .

Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.

54,33333… – периодическая чистая десят.дробь

2,5621212121… – периодическая смешанная дробь

Примеры записи бесконечных десятичных дробей:

Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.

Перевод периодических десятичных дробей в обыкновенные

Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.

Смешанная периодическая десятичная дробь переводится следующим образом:

нужно сформировать число, состоящее из числа, стоящего после запятой до периода, и первого периода;
из полученного числа вычесть число, стоящее после запятой до периода. Итог составит числитель обыкновенной дроби;
в знаменателе требуется вписать число, состоящее из кол-ва девяток, равных кол-ву цифр периода, а за ними нулей, кол-во которых равно количеству цифр числа, стоящего после запятой до 1-го периода.

Сравнение десятичных дробей

Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.

Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.

Поскольку

, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.

Сложение и вычитание десятичных дробей

Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.

Умножение десятичных дробей

Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n

Эти действия просты и сводятся к переносу десятичной запятой. При умножении запятая переносится вправо (дробь увеличивается) на количество знаков, равных количеству нулей в 10 n , где n – произвольная целая степень. То есть некоторое количество цифр переносится из дробной части в целую. При делении, соответственно, запятая переносится влево (число уменьшается), и некоторая часть цифр переносится из целой части в дробную. Если цифр для переноса оказывается недостаточно, то недостающие разряды заполняются нулями.

Деление десятичной дроби и целого числа на целое число и на десятичную дробь

Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Для деления десят.дроби (или целого числа) на десят.число необходимо домножить делимое и делитель на число 10 n , в котором количество нулей равно количеству цифр после десят.запятой в делителе. Таким способом избавляются от десят.запятой в дроби, на которую требуется делить. Далее процесс деления совпадает с описанным выше.

Графическое представление десятичных дробей

Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.

Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.

Дроби

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.

Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби , например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее - знаменателем. Если вы постоянно путаете эти названия (бывает...), скажите себе с выражением фразу: "Ззззз апомни! Ззззз наменатель - вниззззз у!" Глядишь, всё и ззззапомнится.)

Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления - две точки.

Когда деление возможно нацело, это надо делать. Так, вместо дроби "32/8" гораздо приятнее написать число "4". Т.е. 32 просто поделить на 8.

32/8 = 32: 8 = 4

Я уж и не говорю про дробь "4/1". Которая тоже просто "4". А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби , например:

Именно в таком виде нужно будет записывать ответы на задания "В".

3. Смешанные числа , например:

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните... На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !

Основное свойство дроби.

Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:

Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.

А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но... человек - существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.

Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .

Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.

Например, надо упростить выражение:

Тут и думать нечего, зачеркиваем букву "а" сверху и двойку снизу! Получаем:

Все правильно. Но реально вы поделили весь числитель и весь знаменатель на "а". Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть "а" в выражении

и получить снова

Что будет категорически неверно. Потому что здесь весь числитель на "а" уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!

Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё... пока сокращается, короче. Получим 3/8! Куда приятнее, правда?

Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?

Как переводить дроби из одного вида в другой.

С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.

А если целых - не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель - то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .

А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.

Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела "В" получилось 1/2? Что в ответ писать будем? Там десятичные требуются...

Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно...)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.

Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000... Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.

А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333... Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !

Кстати, это полезная информация для самопроверки. В разделе "В" в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.

Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками... Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.

Пусть в задачке вы с ужасом увидели число:

Спокойно, без паники соображаем. Целая часть - это 1. Единица. Дробная часть - 3/7. Стало быть, знаменатель дробной части - 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:

Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.

Обратная операция - перевод неправильной дроби в смешанное число - в старших классах редко требуется. Ну если уж... И если Вы - не в старших классах - можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.

Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?

Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !

Если в задании сплошь десятичные дроби, но гм... злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?

0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!

Подведём итоги этого урока.

1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.

2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.

3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное - перейти к обыкновенным дробям.

Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Должны получиться вот такие ответы (в беспорядке!):

На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего...) Если уж кто совсем крепко забыл, или ещё не освоил... Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

В виде:

± d m … d 1 d 0 , d -1 d -2 …

где ± — знак дроби: или +, или -,

, — десятичная запятая, которая служит разделителем меж целой и дробной частями числа,

d k — десятичные цифры.

При этом порядок следования цифр до запятой (слева от неё) имеет конец (как min 1-на цифра), а после запятой (справа) — может быть и конечной (как вариант, цифр после запятой может вообще не быть), и бесконечной.

Значением десятичной дроби ± d m … d 1 d 0 , d -1 d -2 … есть действительное число:

которое равно сумме конечного либо бесконечного количества слагаемых.

Представление действительных чисел при помощи десятичных дробей есть обобщение записи целых чисел в десятичной системе счисления. В представлении целого числа десятичной дробью нет цифр после запятой, и т.о., это представление выглядит так:

± d m … d 1 d 0 ,

И это совпадает с записью нашего числа в десятичной системе счисления.

Десятичная дробь - это итог деления 1-цы на 10, 100, 1000 и так далее частей. Эти дроби довольно удобны для вычислений, т.к. они основываются на такой же позиционной системе , на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями практически такие же, как и для целых чисел.

Записывая десятичные дроби не нужно отмечать знаменатель, он определяется местом, занимаемым соответствующей цифрой. Вначале пишем целую часть числа, далее справа ставим десятичную точку. Первая цифра после десятичной точки обозначает число десятых, вторая - число сотых, третья - число тысячных и так далее. Цифры, которые расположены после десятичной точки, являются десятичными знаками .

Например:

Одно из преимуществ десятичных дробей таково, что их очень просто можно привести к виду обыкновенных: число после десятичной точки (у нас это 5047) - это числитель ; знаменатель равен n -ой степени 10, где n - число десятичных знаков (у нас это n = 4 ):

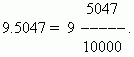
Когда в десятичной дроби нет целой части, значит, перед десятичной точкой ставим нуль:

Свойства десятичных дробей.

1. Десятичная дробь не изменяется, когда справа добавляются нули:

13.6 =13.6000.

2. Десятичная дробь не изменяется, когда удаляются нули, которые расположены в конце десятичной дроби:

0.00123000 = 0.00123.

Внимание! Нельзя удалять нули, которые расположенные НЕ в конце десятичной дроби!

3. Десятичная дробь увеличивается в 10, 100, 1000 и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 2 и так далее позиций правее:

3.675 → 367.5 (дробь увеличилась в сто раз).

4. Десятичная дробь становится меньше в десять, сто, тысячу и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 3 и так далее позиций левее:

1536.78 → 1.53678 (дробь стала меньше в тысячу раз).

Виды десятичных дробей.

Десятичные дроби делятся на конечные , бесконечные и периодические десятичные дроби .

Конечная десятичная дробь - это дробь, содержащая конечное количество цифр после запятой (или их там нет совсем), т.е. выглядит так:

Действительное число можно представить как конечную десятичную дробь лишь в том случае, если это число есть рациональным и при записи его несократимой дробью p/q знаменатель q не имеет простых делителей, которые отличны от 2 и 5.

Бесконечная десятичная дробь .

Содержит бесконечно повторяющуюся группу цифр, которая называется периодом . Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345) .

Периодическая десятичная дробь - это такая бесконечная десятичная дробь, в которой последовательность цифр после запятой, начиная с некоторого места, является периодически повторяющейся группой цифр. Иными словами, периодическая дробь — десятичная дробь, выглядящая так:

Подобную дробь обычно кратко записывают так:

Группа цифр b 1 … b l , которая повторяется, является периодом дроби , число цифр в этой группе является длиной периода .

Когда в периодической дроби период идет сразу после запятой, значит, дробь является чистой периодической . Когда между запятой и 1-ым периодом есть цифры, то дробь является смешанной периодической , а группа цифр после запятой до 1-го знака периода — предпериодом дроби .

Например , дробь 1,(23) = 1,2323… есть чистой периодической, а дробь 0,1(23)=0,12323… — смешанной периодической.

Основное свойство периодических дробей , благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и лишь они представляют рациональные числа . Точнее, имеет место следующее:

Любая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, когда рациональное число раскладывается в бесконечную десятичную дробь, значит, эта дробь будет периодической.

Десятичные дроби - это те же самые обыкновенные дроби, но в так называемой десятичной записи. Десятичная запись используется для дробей со знаменателями 10, 100, 1000 и т. д. При этом вместо дробей 1/10; 1/100; 1/1000; ... пишут 0,1; 0,01; 0,001;... .

К примеру, 0,7 (ноль целых семь десятых ) - это дробь 7/10; 5,43 (пять целых сорок три сотых ) - это смешанная дробь 5 43/100 (или, что то же самое, неправильная дробь 543/100).

Может случиться так, что сразу после запятой стоит один или несколько нулей: 1,03 - это дробь 1 3/100; 17,0087 - это дробь 17 87/10000. Общее правило таково: в знаменателе обыкновенной дроби должно быть столько нулей, сколько цифр стоит после запятой в записи десятичной дроби .

Десятичная дробь может оканчиваться на один или несколько нулей. Оказывается, эти нули «лишние» - их можно попросту убрать: 1,30 = 1,3; 5,4600 = 5,46; 3,000 = 3. Сообрази, почему это так?

Десятичные дроби естественным образом возникают при делении на «круглые» числа - 10, 100, 1000, ... Обязательно разберись в следующих примерах:

27:10 = 27/10 = 2 7/10 = 2,7;

579:100 = 579/100 = 5 79/100 = 5,79;

33791:1000 = 33791/1000 = 33 791/1000 = 33,791;

34,9:10 = 349/10:10 = 349/100 = 3,49;

6,35:100 = 635/100:100 = 635/10000 = 0,0635.

Замечаешь ли ты здесь некую закономерность? Попробуй ее сформулировать. А что будет, если умножить десятичную дробь на 10, 100, 1000?

Чтобы перевести обыкновенную дробь в десятичную, нужно привести ее к какому-нибудь «круглому» знаменателю:

2/5 = 4/10 = 0,4; 11/20 = 55/100 = 0,55; 9/2 = 45/10 = 4,5 и т. д.

Складывать десятичные дроби намного удобнее, чем дроби обыкновенные. Сложение производится так же, как и с обычными числами - по соответствующим разрядам. При сложении в столбик слагаемые нужно записывать так, чтобы их запятые находились на одной вертикали. На этой же вертикали окажется и запятая суммы. Совершенно аналогично выполняется и вычитание десятичных дробей.

Если при сложении или вычитании в одной из дробей количество цифр после запятой меньше, чем в другой, то в конце данной дроби следует дописать нужное число нулей. Можно эти нули и не дописывать, а просто представить их себе в уме.

При умножении десятичных дробей их опять-таки следует перемножить как обычные числа (при этом уже не обязательно записывать запятую под запятой). В полученном результате нужно отделить запятой количество знаков, равное суммарному числу знаков после запятой в обоих множителях.

При делении десятичных дробей можно в делимом и делителе одновременно передвинуть запятую вправо на одно и то же количество знаков: частное от этого не изменится:

2,8:1,4 = 2,8/1,4 = 28/14 = 2;

4,2:0,7 = 4,2/0,7 = 42/7 = 6;

6:1,2 = 6,0/1,2 = 60/12 = 5.

Объясни, почему это так?

Нарисуй квадрат 10x10. Закрась какую-нибудь его часть, равную: а) 0,02; б) 0,7; в) 0,57; г) 0,91; д) 0,135 площади всего квадрата.
Что такое 2,43 квадрата? Изобрази на рисунке.
Раздели на 10 числа 37; 795; 4; 2,3; 65,27; 0,48 и результат запиши в виде десятичной дроби. Эти же числа раздели на 100 и на 1000.
Умножь на 10 числа 4,6; 6,52; 23,095; 0,01999. Эти же числа умножь на 100 и на 1000.
Представь десятичную дробь в виде обыкновенной дроби и сократи ее:
а) 0,5; 0,2; 0,4; 0,6; 0,8;
б) 0,25; 0,75; 0,05; 0,35; 0,025;
в) 0,125; 0,375; 0,625; 0,875;
г) 0,44; 0,26; 0,92; 0,78; 0,666; 0,848.
Представь в виде смешанной дроби: 1,5; 3,2; 6,6; 2,25; 10,75; 4,125; 23,005; 7,0125.
Представь обыкновенную дробь в виде десятичной дроби:
а) 1/2; 3/2; 7/2; 15/2; 1/5; 3/5; 4/5; 18/5;
б) 1/4; 3/4; 5/4; 19/4; 1/20; 7/20; 49/20; 1/25; 13/25; 77/25; 1/50; 17/50; 137/50;
в) 1/8; 3/8; 5/8; 7/8; 11/8; 125/8; 1/16; 5/16; 9/16; 23/16;
г) 1/500; 3/250; 71/200; 9/125; 27/2500; 1999/2000.
Найди сумму: а) 7,3+12,8; б) 65,14+49,76; в) 3,762+12,85; г) 85,4+129,756; д) 1,44+2,56.
Представь единицу в виде суммы двух десятичных дробей. Найди еще двадцать способов такого представления.
Найди разность: а) 13,4–8,7; б) 74,52–27,04; в) 49,736–43,45; г) 127,24–93,883; д) 67–52,07; е) 35,24–34,9975.
Найди произведение: а) 7,6·3,8; б) 4,8·12,5; в) 2,39·7,4; г) 3,74·9,65.

В швейной мастерской было 5 цветов ленты. Красной ленты было больше, чем синей на 2,4 метра, но меньше, чем зеленой на 3,8 метра. Белой ленты было больше, чем черной на 1,5 метра, но меньше, чем зеленой на 1,9 метра. Сколько метров ленты всего было в мастерской, если белой было 7,3 метра?

Решение

1) 7,3 + 1,9 = 9,2 (м) зеленой ленты было в мастерской;
2) 7,3 – 1,5 = 5,8 (м) черной ленты;
3) 9,2 – 3,8 = 5,4 (м) красной ленты;
4) 5,4 - 2,4 = 3 (м) синей ленты;
5) 7,3 + 9,2 + 5,8 + 5,4 + 3 = 30,7 (м).
Ответ: всего в мастерской было 30,7 метров ленты.

Задача 2

Длина прямоугольного участка составляет 19,4 метра, а ширина на 2,8 метра меньше. Вычислите периметр участка.

Решение

1) 19,4 – 2,8 = 16,6(м) ширина участка;
2) 16,6 * 2 + 19,4 * 2 = 33,2 + 38,8 = 72(м).
Ответ: периметр участка равен 72 метра.

Задача 3

Длина прыжка кенгуру может достигать 13,5 метров в длину. Мировой рекорд для человека составляет 8,95 метров. Насколько дальше прыгает кенгуру?

Решение

1) 13,5 – 8,95 = 4,55 (м).
2) Ответ: кенгуру прыгает на 4,55 метра дальше.

Задача 4

Самая низкая температура на планете была зарегистрирована на станции Восток в Антарктиде, летом 21 июля 1983 года и составляла -89,2 ° C, а самая жаркая в городке Эль-Азизия, 13 сентября 1922 года составляла +57,8 ° C. Вычисли разницу между температурами.

Решение

1) 89,2 + 57,8 = 147° C.
Ответ: разница между температурами составляет 147° C.

Задача 5

Грузоподъемность фургона Газель составляет 1,5 тонн, а карьерного самосвала БелАЗ в 24 раза больше. Вычислите грузоподъемность самосвала БелАЗ.

Решение

1) 1,5 * 24 = 36 (тонн).
Ответ: грузоподъемность БелАЗа 36 тонн.

Задача 6

Максимальная скорость движения Земли по своей орбите 30,27 км/сек, а скорость Меркурия на 17,73 км больше. С какой скоростью Меркурий движется по своей орбите?

Решение

1) 30,27 + 17,73 = 48 (км/сек).
Ответ: скорость движение Меркурия по орбите 48 км/сек.

Задача 7

Глубина Марианской впадины составляет 11,023 км, а высота самой высокой горы в мире - Джомолунгмы 8,848 км над уровнем моря. Вычисли разницу между этими двумя точками.

Решение

1) 11,023 + 8,848 = 19,871(км).
Ответ: 19, 871 км.

Задача 8

Для Коли, как и для любого здорового человека, нормальная температура тела 36,6 ° C, а для его четвероногого друга Шарика на 2,2 ° C больше. Какая температура для Шарика считается нормальной?

Решение

1) 36,6 + 2,2 = 38,8° C.
Ответ: для Шарика нормальная температура тела 38,8° C.

Задача 9

Маляр за 1 день покрасил 18,6 м² забора, а его помощник, на 4,4 м² меньше. Сколько всего м2 забора покрасит маляр и его помощник за рабочую неделю, если она равна пяти дням?

Решение

1) 18,6 – 4,4 = 14,2 (м²) покрасит за 1 день помощник маляра;
2) 14,2 + 18,6 = 32,8 (м²) покрасят за 1 день вместе;
3) 32,8 *5 = 164 (м²).
Ответ: за рабочую неделю маляр и его помощник вместе покрасят 164 м² забора.

Задача 10

От двух пристаней навстречу друг другу одновременно отошли два катера. Скорость одного катера 42,2 км/ч второго на 6 км/ч больше. Какое расстояние будет между катерами через 2,5 часа, если расстояние между пристанями 140,5 км?

Решение

1) 42,2 + 6 = 48,2 (км/ч) скорость второго катера;
2) 42,2 * 2,5 = 105,5 (км) преодолеет первый катер за 2,5 часа;
3) 48,2 * 2,5 = 120,5 (км) преодолеет второй катер за 2,5 часа;
4) 140,5 – 105,5 = 35 (км) расстояние от первого катера до противоположной пристани;
5) 140,5 – 120, 5 = 20 (км) расстояние от второго катера до противоположной пристани;
6) 35 + 20 = 55 (км);
7) 140 – 55 = 85 (км).
Ответ: между катерами будет 85 км.

Задача 11

Каждый день велосипедист преодолевает 30,2 км. Мотоциклист, если бы затрачивал столько же времени, преодолевал бы расстояние в 2,5 раза большее, чем велосипедист. Какое расстояние может преодолеть мотоциклист за 4 дня?

Решение

1) 30,2 * 2,5 = 75,5 (км) за 1 день преодолеет мотоциклист;
2) 75,5 * 4 = 302 (км).
Ответ: мотоциклист может преодолеть за 4 дня 302 км.

Задача 12

В магазине за 1 день было продано 18, 3 кг печенья, а конфет на 2,4 кг меньше. Сколько конфет и печенья вместе было продано в магазине за этот день?

Решение

1) 18,3 – 2, 4 = 15,9 (кг) конфет было продано в магазине;
2) 15,9 + 18,3 = 34,2 (кг).
Ответ: конфет и печенья всего было продано 34,2 кг.